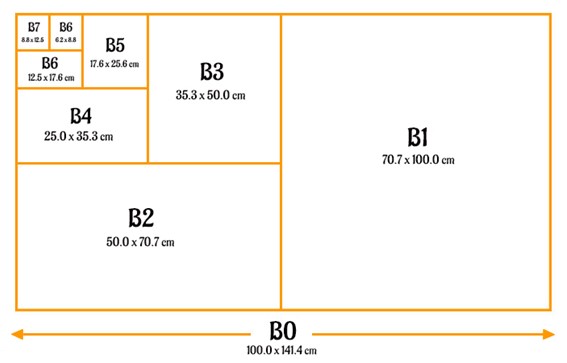
Series B Paper Size Chart
| B Paper Size | Dimensions (inches) | Dimensions (mm) | Area (mm²) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| B0 Size | 39.4 × 55.7 | 1000 × 1414 | 1414000 | ||||||
| B1 Size | 27.8 × 39.4 | 707 × 1000 | 707000 | ||||||
| B2 Size | 19.7 × 27.8 | 500 × 707 | 353500 | ||||||
| B3 Size | 13.9 × 19.7 | 353 × 500 | 176500 | ||||||
| B4 Size | 9.8 × 13.9 | 250 × 353 | 88250 | ||||||
| B5 Size | 6.9 × 9.8 | 176 × 250 | 44000 | ||||||
| B6 Size | 4.9 × 6.9 | 125 × 176 | 22000 | ||||||
| B7 Size | 3.5 × 4.9 | 88 × 125 | 11000 | ||||||
| B8 Size | 2.4 × 3.5 | 62 × 88 | 5456 | ||||||
| B9 Size | 1.7 × 2.4 | 44 × 62 | 2728 | ||||||
| B10 Size | 1.2 × 1.7 | 31 × 44 | 1364 | ||||||
| Series B Paper Size Chart Maker : iSizeChart.com | |||||||||
About Series B Paper Size Chart
How are the B series paper sizes defined?
The B series paper sizes, standardized in ISO 216, are defined as the geometric mean between corresponding sizes in the A series. This gives them a unique purpose: providing intermediate sizes where A series sheets might be too small or too large. Here's the precise definition:
1. Core Principles.
The largest size, B0, has a width of 1 meter (1000 mm).
Its height maintains the aspect ratio 1:√2 (≈1:1.4142).
②. Constant Aspect Ratio:
Like the A series, all B sizes have an aspect ratio of 1:√2. Halving the longer side produces the next smaller size with the same ratio.
③. Geometric Mean Relationship:
A B size is the geometric mean between its corresponding A size and the previous A size.
Mathematically:
B𝑛 = Geometric Mean(A𝑛, A(𝑛-1))
→ Width(B𝑛) = √(Width(A𝑛) × Width(A(𝑛-1)))
→ Height(B𝑛) = √(Height(A𝑛) × Height(A(𝑛-1)))
Example: B1 is the geometric mean of A1 and A0.
2. Deriving Dimensions.
Width = 1000 mm; Height = 1000 mm × √2 ≈ 1414 mm (rounded to mm); B0 = 1000 mm × 1414 mm.
②. Deriving Smaller Sizes (via Halving):
Apply the same halving rule as the A series:
B1: Halve the longer side (height) of B0. 1000 mm × (1414 mm / 2) = 1000 mm × 707 mm.
B2: Halve the longer side of B1. (1000 mm / 2) × 707 mm = 500 mm × 707 mm.
Continue down to B10.
③. Relationship to A Series (Geometric Mean):
B1 = √(A1 × A0) = √(594×841) ≈ √499,554 ≈ 707 mm (height). Width = 707 / √2 ≈ 500 mm → Matches halving method.
B4 = √(A4 × A3) = √(210×297) ≈ √62,370 ≈ 250 mm (width). Height = 250 × √2 ≈ 354 mm → B4 = 250 mm × 354 mm.
3. Key Characteristics & Purpose.
Envelopes & Folders: Primarily used for envelopes (C series envelopes match B series paper). Example: A C4 envelope holds an unfolded A4 sheet; a B4 envelope holds A4 folded once or A3 unfolded.
Books & Posters: Common for books, passports (B7 is standard), posters, and wall charts where A sizes aren't ideal.
Scaling Flexibility: The geometric mean ensures consistent scaling: Enlarging A4 (210x297) to B4 (250x354) = ~119% scale. Reducing B4 to A4 = ~84% scale.
Tolerances & Rounding: Follows ISO 216 specs (similar to A series: ±1-1.5 mm for large sheets, ±0.5 mm for smaller ones).
4. Why B Series Exists.
Efficient Scaling: Allows smooth transitions between A sizes without custom scaling.
International Standard: Ensures compatibility in printing, publishing, and design globally (except regions using ANSI sizes).
Historical Note: Like the A series, the B series' aspect ratio was proposed by Georg Lichtenberg (1786) and later adopted in early French and German standards before ISO 216.
The B series complements the A series, creating a versatile system where each size has a clear purpose and mathematical relationship.